OBJECTIVES:
The objective of this project is to learn the important role of mathematical models of physical system of cruice control and then stabilize and the design PID controller and analysis of  system using MATLAB.

ANALYSIS:

In this Project we are going to analyze mathematical model transfer function and PID of Ball and Beam system.

PROCEDURE :

 Introduction

The ball and beam systems also called ‘balancing a ball on a beam’. It can usually be found in most university control labs. It is generally linked to real control problems such as horizontally stabilizing an airplane during landing and in turbulent airflow. The significance of the ball and beam system is that it is a simple system which is open-loop unstable. Even if the beam is restricted to be very nearly horizontal, without activefeedback, it will swing to one side or the other, and the ball will roll off the end of the beam. To stabilize the ball, and to to control the position of the ball to a desired reference point, and reject disturbances a control system which measures the position of the ball and adjusts the beam accordingly must be used.

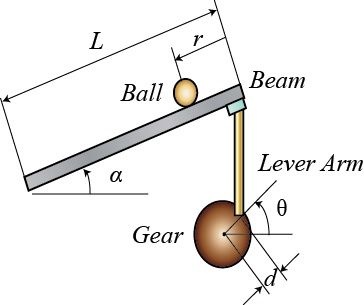
Physical setup and Lagrangian equation of system:

We define some parameters by assigning constant value and then write Lagrangian equation of a system  mass of the ball  =m= 0.11 kg, radius of the ball=r= 0.015 m, lever arm offset=d= 0.03 m,gravitational acceleration=g= 9.8 m/s^2, length of the beam =L= 1.0 m, ball's moment of inertia=J= 9.99e-6 kg.m^2, ball position coordinate=r, (alpha)  beam angle coordinate,(theta)  servo gear angle

The langrangian equation for this system is defined as

When we linearize this equation at alpha is equal to zero                                                                                                                         

                     equation 1                                                            

The equation which relates the beam angle to the angle of the gear can be approximated as linear by the equation below:

 Sinα/ Sinθ=d/L

We consider Sinα=α and Sinθ=θ now putting this value in above equation

α/ θ=d/L

α= θd/L

now put this value in equation 1

we get

Now we take laplace transform of this equation

We get,

Now we rearrange this equation in order to get transfer function  in  the  forward  loop  of  the  process.