In the mind's eye, a fractal is a way of seeing infinity. – James Gleick
Who Discovered Fractal Geometry?
"Benoît B. Mandelbrot was a French-American scientist with a special interest in the art of roughness of physical phenomena and the uncontrolled element in life. He referred to himself as fractalist."

A fractal work of art showing the sunrise on a strange world out there in deep space.
Biography of Benoît B. Mandelbrot
His Early Years
Benoît B. Mandelbrot was born November 20, 1924 in Warsaw, Poland. His father was a scientist and the descendant of a line of academics. In fact, in his family everyone was expected to become an academic of some kind. However, his father was a starving academic and he preferred a good steady job as a tailor.
His mother was a doctor. Afraid of pandemics, she kept him out of school and he was teached chess and reading fast by a relative at home.
In 1936, his family moved to Paris, where he attended the lycée. During World War II, they lived in the countryside for maximizing their chances to survive the German occupation. By these circumstances, he remained far from the Gymnasium. During this time, he learned mainly autodidactically.
From 1944 to 1947, he studied at the Polytechnic and he graduated as an Engineer. Subsequently, he studied for two years in the USA. Then he spent a year with the French Air Force.
Benoît B. Mandelbrot's Research Career
From 1949 to 1957, he worked in research. Among other things, he helped develop the first Philips color monitor. In 1955, he married his wife Aliette and they moved to Geneva, where they lived until 1957. He worked at the University of Geneva and his task was to teach mathematics. In 1957, they went back to France and Mandelbrot worked at different universities.
Benoît B. Mandelbrot's Years with IBM
However, the important career was the one with IBM. From 1958 to 1974, he was a research staff member at IBM Thomas J. Watson Research Center, Yorktown Heights, New York. From 1974 to 1997, he was an IBM fellow. This honor was a sign that his work was widely respected and that he could continue his own way.
What Mandelbrot researched at IBM
Quotes describing his research subject:
Bottomless wonders spring from simple rules, which are repeated without end.
Benoît B. Mandelbrot
Nobody will deny that there is at least some roughness everywhere.
Benoît B. Mandelbrot
Why is geometry often described as “cold” and “dry?” One reason lies in its inability to describe the shape of a cloud, a mountain, a coastline, or a tree. Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line… Nature exhibits not simply a higher degree but an altogether different level of complexity.
Benoît B. Mandelbrot
Benoît B. Mandelbrot developed the Mandelbrot set in the 1980s and it is astonishing that the Mandelbrot plot is only made of one simple formula in the complex plain.
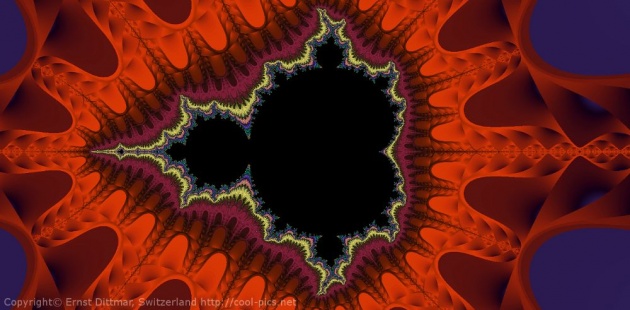
Mandelbrot set.
Benoît B. Mandelbrot's Late Years
Big brains, small films. A short video about Benoît B. Mandelbrot, IBM Fellow Emeritus and father of fractals. The film includes an easy-to-understand explenation of the Mandelbrot Set formula and how the word fractal was created.
Benoît B. Mandelbrot passed away on October 14, 2010. But his work lives on.
What Are Fractals?
Benoît B. Mandelbrot invented the term “fractal” and he defined fractals as follows:
“Fractals are objects, whether mathematical, created by nature or by man, that are called irregular, rough, porous or fragmented. They possess the same properties at any scale. That is to say, they have the same shape, whether seen from close or from far.”
If you understood the above explenation of "fractal", you will also understand the following joke:
What stands the B. for in Benoît B. Mandelbrot?
The B. stands for Benoît B. Mandelbrot.

This is a Julia set, created with the free GIMP image editing software. Benoît B. Mandelbrot experimented with the Julia set in the 1970s, before he discovered the Mandelbrot set in the 1980s.
Some Mathematics: Expect the Unexpected
Chaos theory is a branch of mathematics focused on the behavior of complex systems that are highly sensitive to initial conditions. (Sounds very similar to the the definition of fractals, doesn't it?) The Chaos Theory tells us about surprises, risks, nonlinear procedures and other unpredictable phenomena like the weather, the climate, accidents, road traffic, stock markets, exchange rates, and so on.
Principles of Chaos
Do not worry; I will not go too deep into the Chaos Theory. However, knowing about some principles of chaos will be helpful for understanding the fractal geometry later in this blog.
Two neighboring water molecules may end up in different oceans as turbulences happen at all scales. Fluids can be mixed. However, they cannot be unmixed.
Feedback can cause complex systems to become chaotically. Such an example is the foreign exchange market. Depending whether a currency’s price is increasing or decreasing, the market players buy or sell that currency. If the masses follow each other like lemmings and buy it or sell it in excess, the exchange rates can become much chaotically.
The Butterfly Effect grants the power to cause a typhoon in South-East Asia to the flap of a wing of a butterfly in the USA. This connection is real and it describes the fact that small changes in the initial conditions can cause dramatic results. Without the butterfly flapping its wings, the typhoon would not have happened.
We never know the perfect details of the initial conditions of a complex system. Therefore, we can never predict the results of such a system.
Chaos is not a clearly defined state of order or disorder. Chaos is also about the transitions between order and disorder. Often, these transitions happen in a much-unexpected way.
Fractal Geometry
Phenomena of complex systems and chaos are often explained by fractal geometry. Fractals are never ending complex patterns, which are self-similar at any scale. Benoît B. Mandelbrot constructed the hypothesis that fractal geometry could explain the infinite complexity of nature with a simple formula. Many natural objects have fractal properties, such as trees, clouds, islands, organs, lakes, flowers, and so on. There are some complex systems around us, which show also a chaotic behavior and follow fractal rules, or they have at least an approximately fractal behavior.
Linearity and Nonlinearty
Linear Phenomena
In this chapter, we look at a piece of a system and we try to determine, what this piece is doing next. If it is not influenced by what it is doing right now, we speak of Linearity. Linear objects enjoy a relatively simple geometry.
Nonlinear Phenomena
Chaos and other such phenomena are absent in linear problems and therefore we call them nonlinear phenomena. In nonlinear systems, the result is depending to what a piece of this system is doing right now. This is called feedback.
What is the Relationship between Chaos and Fractals?
You know quite a lot about fractals and about chaos now. However, did you get the point, how both relate to each other? - If not, do not worry. You are not alone.
“In the nonlinear sciences, fractals and chaos, have different origins, but they are the nonequilibrium process and results which are described by nonlinear equations, indicating that they share a common mathematics ancestor – Dynamical Systems, strange attractors is the fractal sets, or chaos is fractal in time, and fractal is chaos in space.”
Source: http://slideplayer.com/slide/7341765/ Slide 62 of 70 .
If you are none the wiser now, it is not your fault. These are young sciences and many scientists are searching for the universal law of nature. There are not yet universal terms to describe the whole fractal geometry and/or the chaos theory. Both are still fields of future discoveries. We are walking our personal curiosity along the edge of the contemporary human knowledge.
Zooming into a Mandelbrot set. Without a cut, the video is zooming in for full eleven minutes. The zoom-factor is more than 1,000,000. Imagine a zoom-lens on a camera of this zoom factor!
The screen capture was taken live and the left button of the mouse had to be clicked for zooming in. The movements of the mouse are for navigating the fractal image up, down, right and left.
Fractals in Nature
Benoît B. Mandelbrot constructed the hypothesis that fractal geometry could explain the infinite complexity of nature with a simple formula. He observed many such amazing fractals in nature and described them by images as well as by mathematics.

Stockphoto under the global license of fotolia.com
This picture shows the fractal nature of a cabbage. At any scale, we get the same fractal pattern.

Stockphoto under the global license of fotolia.com
The above photo of a romanesco broccoli shows also the same fractal pattern at any scale.

Benoît B. Mandelbrot also recognized fractal patterns in a tree.
Applying Chaos Theory and Fractal Geometry by Artists
“A brief look at history reveals a deep underlying relationship between the inspirations and aspirations of mathematicians, scientists, and artists. For one thing, we are all trying to explain the world around us.” – Steev Morgan
Steev Morgan wrote a great historic article about how chaos theory applied to artistic and cultural practice. I recommend this article to everybody who is interested into history, science and art.
http://www.steev.ca/chaos-in-art-and-cultural-practice/

The land of thornes and spines.
A fractal artwork and an example of a fantasy landscape.
Contemporary Fractal Art

A fractal flower with more flowers on spheres, which are floating quietly through space and time.
Fractal art has developed to an art movement of its own. A steadily growing community of fractal artists is contributing artworks of an outstanding beauty. Most of these people are creating fractal art by the help of their computers.

A lovely blue-beige structure with haze and fog. This landscape could be inside a cave and some daylight is shining through the entrance of the hidden place.
This image was created with Mandelbulb 3D, a sofisticated fractal software with many ways to add lights, haze, fog and daylight to the scene.
There are some great programs available for creating stunning fractal images. However, only a steep learning curve will lead to real mastership in fractal arts. Artists can still develop and discover a whole range of new artistic ways in this young fractal art movement. Right now, many artists are busy with creating 3D fractal objects and landscapes. There is still a wide-open field of developmental possibilities.

Alien settlement in deep space.
A fractal artwork created with Mandelbulb 3D.
You have probably already seen fractal artworks. In science-fiction and fantasy movies, the landscapes are often created by fractal artists.



