Intervisibility of Triangulation Station (T/Station): It is ascertained from the results of reconnaissance by one of the following methods:By joining the two T/Stations’ points with a straight line drawn on the contour map prepared during reconnaissance and comparing the height of LOS between the T/Stations with the intervening ground, whether LOS between the least high T/Stations is clear of ground By making observations from the hills, mounds and climbing the trees Reflecting the light of strong sunlight from high quality mirrors at e.g. one T/Station and observing the quality of gleam from the surrounding T/Stations If the distance between the two T/Stations is large, then the difference in elevation of the (ground of) T/Stations and surrounding ground must also be large. So that the T/Stations must be clearly visible from each other T/Stations; ground and features of the surrounding ground must not get confused with those of the T/Stations and produce the error in taking readings.

Distance of Visible Horizon: If there is no obstruction, the distance D of Visible Horizon from the station A (an Equipment Station usually of known elevation above the MSL), is calculated from the following equation: H = [D2(1 – 2m)]/2R  D = 3.85H      Where H is the height of the Equipment Station above a datum. D is the (curved) distance of Visible Horizon in km; R is the average radius of earth which is taken as 6367 km and ‘m’ is the mean coefficient of refraction which is assumed as 0.07 over the land and 0.08 over the sea.

Visible Horizon: It is a distance between the Equipment Station and a far-off boundary-line; all this area (usually) appears to be a flat horizontal ground, as visible to a surveyor Equation for Intervisibility NOT obstructed by the intervening ground: Suppose, elevation of the Equipment Station A is HA which is known. HB (elevation of a farthest point B) can be found out from the following relation.Let D be the distance of curvature / curved distance formed between the Equipment Station A and the point B which is also a Target.DA be the curved distance between Equipment Station A and

Point of Tangency T.DB be the curved distance between the point T and the point B.We have the relationship between D and H (given on the previous slide):  __ D = 3.85H       DA or B = 3.85HA or B            DA = 3.85HAD = DA + DB     DB = D - DA        HB = (0.067DB)2 Where HB is the vertical distance between the point B and B1 (B1 is the apparent elevated position of point B as appears meeting the horizontal LOS i.e. Plane of Horizon, situated over point B)

Equation for Intervisibility obstructed by the intervening ground: Let C be a point of Obstruction e.g. a hill or mound existing between the Equipment Station A and Point of Tangency T (Point of Tangency is a point where the curvature of Earth appears meeting the horizontal LOS / Plane of Horizon). Point B is situated beyond the point T on the Plane of Horizon.    

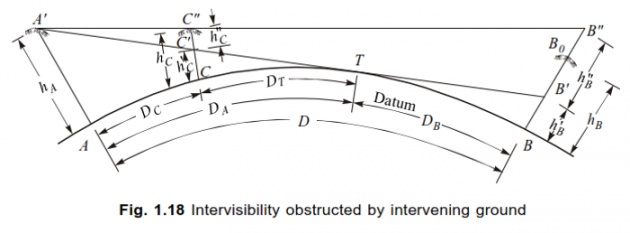
 Suppose C obstructs the LOS; the following procedure is followed: Distance i.e. length of the curve AB = D and D = DA + DB (as given above).Equation for Intervisibility obstructed by the intervening ground: Again DA = DC + DT  DC is the curved distance between the Equipment Station A and obstruction-point C actually located on Earth.    And DT is the curved distance between the obstruction-point C and point T.DA = 3.85 HA (as given in previous slide). Now CT = DA - DC = DT HB = (0.067DB)2 (as given in previous slide)HC = (0.067DC)2  HC is the vertical distance between the point C and C1 (apparent elevated position of point C as appears meeting the horizontal LOS, over point C).

   Vertical distance B1B2  = HB – HB2 = HB1 (B1 is the apparent elevated position of point B; B2 is the apparent elevated position of point B1 lying further above; elevation increases onward B, B1 and B2. HB, HB1 and HB2 are the vertical distances of the points B, B1 and B2; these vertical distances increase onward too)Similarly we assume the two points C1 and C2 in the same way as we established the apparent points B1 and B2 above the actual point B.From the similar isosceles triangles A1C2C1 and A1B2B1 (Refer to . (The elevation increases onward C, C1 and C2 ): We get: B1B2 / C1C2 = D / DC     C1C2 = (B1B2) / (DC / D) where D is the horizontal distance between A and B, and DC is the horizontal distance between A and C, located on  The elevation of LOS at point C2 = CC1 + C1C2 . Equation for Intervisibility obstructed by the intervening ground: If the LOS at C2 is higher than RL of point C, then the LOS will be clear of obstruction otherwise the target at point B will be required to be raised in its elevation. 

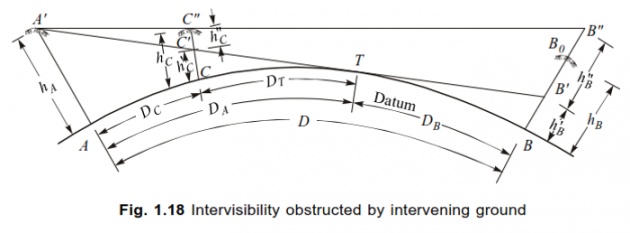
McCaw’s Method:  Captain G T McCaw (a British Geodetic Survey Engineer) developed a method in 1935 to determine whether a LOS is clear of obstruction or not. Let C be a point of Obstruction e.g. a hill or mound existing between the Equipment Station A and a very far-off point B.Now A1 is the elevated position of point A (point A is assumed to be situated on Earth’s curvature i.e. surface), C1 is the elevated position of point C (point C is assumed to be situated on Earth’s curvature i.e. surface) and B1 is the elevated position of point B (point B is assumed to be situated on Earth’s curvature i.e. surface).HA is the elevation of point A from its original actual position on Earth, HC is the elevation of point C from its original actual position on Earth, and HB is the elevation of point B from its original actual position on Earth.  Now the distance AB i.e. the curved length AB = 2S And AB = AC + CB = (S + d) + (S – d) = 2S Distance AC i.e. the curved length AC = S + d (McCaw’s assumption)Distance CB i.e. the curved length CB = S - d (McCaw’s assumption) Let ξ (Zii; eq to X of English) be the Zenith Distance i.e. 90o – vertical angle under consideration).McCaw’s Formula states that: Height HC of LOS at the point C is:HC = ½ (HB + HA) + ½ (HB - HA).(d) – (S2 – d2).(1 – 2m) Cosec2ξ ….. (i)                                                      S                        2RAnd Value of Zenith Distance is given by the following relation:Cosec2ξ = 1 + (HB + HA)2 In most of the practical surveys, this distance                              4S2        (Zenith Distance) is assumed to be very close to unity  Cosec2ξ = 1, making (HB + HA)2 /4S2 = 0. Putting the values of m and R in (1 – 2m)/2R, this term becomes = 0.067 in the equation (i).Therefore, the height of obstructive point C, HC comes to be:HC = ½ (HB + HA) + ½ (HB - HA).(d/S) – (S2 – d2) x 0.067 x 1 ……. (ii)Above-given equation (ii) is a deciding equation to calculate the height of obstructive point C, HC, whether the LOS is clear of this obstructive point C or the (target at) point B is required to be raised.