Braced Quadrilaterals:
It looks like a chain of quadrilaterals containing X-like diagonals in them; the said quadrilaterals are joined up and down (or side by side) forming a chain like configuration.
This method is widely used. It allows the measurements of lengths of the triangles enclosed in this type, different routes.
Centred Triangles and Polygons:
It looks like a network of various (usually) pentagons joined side by side either in a horizontal, vertical or zig-zag line; each element has got a central point with the lines radiating towards the vertices.
It is used when the area is very large in all the directions.
Progress is very slow because Theod is to be set up on a number of points.
Combination of the above:
Depending upon the shape, area and accuracy, more than one above-given methods may be used for Triangulation Surveying.

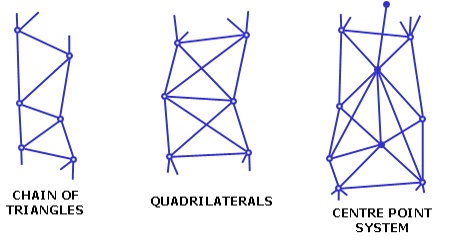
Layout of Primary Triangles:
Two types of Layouts are used (for extremely large area e.g. a country or province): (i) Grid-Iron System (ii) Central System
(i) Grid-Iron System: It looks like a series of triangles laid along the perimeter of some regular figure, along a square or rectangle.
Main alignment of the triangles is usually along N – S or / and E – W meridian.
(ii) Central System: It looks like an almost unlimited number of triangles enclosed between a regular (or irregular) circle, oval or semi-oval.
The triangulation network (network of a huge number of triangles are packed side by side / filled in e.g. a regular circle) appears as initiating from a central point (which is usually the centre of a country, country’s capital or centre of the province or province’s capital) and extends in all the directions usually uniformly, in form of series of (unlimited number of) triangles.
Well-Conditioned Triangle included in a Triangulation Network:
A triangle in which any error while measuring an angle has a minimum effect upon the computations / computed length of that triangle, is called a Well-Conditioned Triangle.
An equilateral or nearly equilateral triangle i.e. a triangle whose angles are between 55o and 60o, if its all the angles are not of 60o.
Calculating Well-Conditioned Angle i.e. most suitable angle of Well-Conditioned Triangle:
Let us consider an isosceles triangle ABC in which the lengths & angles:
AC = BC = a = b Let A =  B = β and C = Ɣ
A =  = B = β So  = β and  + β = 2

a c
 a / Sin = c / Sin Ɣ  a = cSin / SinƔ ……… (i)

Let δ be a small error in the measurement of angle  which introduces a small error δa1 in the side a. Differentiating the equation (i) with respect to angle  partially, we get: δa1 = (cCosδ/SinƔ) .…….
Dividing eq. (ii) by eq. (i), we get:
δa1 = cCosδ . SinƔ = Cos  . δ = Cotδ  δa1 = Cotδ ………. (iii)
a SinƔ cSin Sin a
Again, let δƔ be a small error in the measurement of angle Ɣ which introduces a small error δa2 in the side a. Differentiating the equation (i) with respect to angle Ɣ partially, we get: δa2 = (cSin).(-1).(CosƔ/Sin2Ɣ)δƔ ... (iv)

Dividing equation (iv) by equation (i), we get:
δa2 = - cSinCosƔδƔ. SinƔ = - CosƔ.δƔ = - CotƔδƔ  δa2 = - CotƔδƔ… (v)
a Sin2Ɣ cSin SinƔ a

If δ = δƔ =  a’ is the probable error in the angles, then the probable error in the side “a” can be found out using Pythagorean Theorem (Pythagoras {Pron: Feesa-gorus}: A Greek Mathematician, formulated this formula in 550 BC) assuming an imaginary Right-Angled Triangle comprising the sides equal to the values of the errors in the side ‘a’:
δa =  (Value of δa1/a)2 + (Value of δa2/a)2

Note that the probable error δa/a will be minimum if the value of
Cot2 + Cot2Ɣ is minimum.

In isosceles triangle ABC:
Ɣ = 180o – ( + β) = 180o – 2 [We have assumed  = β]
_____________________________
Then the eq. (vi) becomes: δa =  a’ Cot2 + Cot2(180o – 2) ……. (vii)

___________________
 δa =   Cot2 + Cot22 ……………...… (viii)

For δa/a to be minimum, Cot2 + Cot22 must be the minimum.

Now differentiating Cot2 + Cot22 with respect to  and equating it to zero, we get: 4Cos4 + 2Cos2 ± 1 = 0 …….. (ix)
[It is either + or – sign; it is to be confirmed]
Solving the equation (ix) for Cos, we get:  = 56o14’

Hence the best shape of an isosceles triangle is that whose both the base angles are 56o14’ each. However, from the practical consideration, an equilateral triangle may be treated as a Well-Conditioned Triangle. In actual triangulation practice, the triangles having an angle less than 30o and greater than 120o must not be considered.
Reconnaissance: It is a preliminary field investigation-procedure of entire area that is to be covered by Triangulation Surveying. Reconnaissance includes the following operations:
A detailed and critical visual examination of the terrain
Noting down the important details, drawing rough sketches and maps usually topographic / contour maps
Taking photos
Selection of suitable Base Lines / Check Lines
Computations / assessment of heights of the towers, signals, poles, etc.
Selection of well-defined natural features as reference points
Collection of miscellaneous / important information relevant to triangulation works e.g. access to triangulation station, other access points, nearby transport facilities, availability of amenities (food, water, shelter, etc), availability of labour, suitable ground to be used for

Selection of (location of) Triangulation Station (T/Station):
T/Stations should be selected on high lands / higher areas, top of hills or mounds to have good intervisibility
A T/Station must be intervisible from all the surrounding T/Stations
T/Stations must be located at the vertex of a well-conditioned triangle
T/Stations should be easily accessible to the transport facilities
T/Stations should be selected in such a way that the distance between them must not be too short or too long
Cost of clearing the LOS to and from the T/Stations should be low e.g. cutting of trees and shrubs, building of tower at a T/Station, etc.
To avoid the refraction, interference or dispersion of the light of LOS, T/Stations should be selected on such locations that the LOS must not pass through the cities / dust, smoke, heat, brilliant dazzling light, etc.