CURVE SURVEYING
Bends are required to be provided in the roads, railways, canals, ducts, pipeline, etc. due to the condition of terrain, surrounding, cultural or any other unavoidable reason or condition. As the radius and length of curve increases, measurement with the tape becomes impractical.
Types of Curves:
(1) Horizontal Curves (located in Horizontal Plane)
(2) Vertical Curves (located in Vertical Plane)
Horizontal Curves: (i) Simple (ii) Compound (iii) Reverse (iv) and Spiral N. B:
Transition Curve is a type of both Horizontal Curve as well as Vertical CurveSimple Curve:
The simple curve is an arc of a circle. It is the most commonly used type of Horizontal Curve.
The radius of the circle determines the “sharpness” or “flatness” of the curve. and easy & comfortable to turn for the vehicles especially long ones
.Compound Curve: (usually of different radii) curving in the same direction and are joined together in a regular curvature.
Reverse Curve: A reverse curve consists of two simple curves joined together but curving in opposite directions. For safety reasons, the designing-engineer must not design this curve unless absolutely necessary
.Spiral Curve: This curve comprises a curved-segment of a certain radius placed between the two curved segments of the same radius having differentradius from that which is located in the centre of the enclosing segments
.Transition Curve: It is a curve whose radius changes regularly (the radius decreases towards the apex and vice-versa).
This curve is usually and necessarily provided in the fast moving transportation paths e.g. Super-highway, Express Highway, Motorway, High Speed Railway, etc. so as to facilitate the comfortable turning of the traffic without getting out of control and thrown away or overturned.
Such curves involve more complex formulas than the curves with a constant radius. N.
B: Transition Curve is a type of both Horizontal Curve as well as Vertical CurveVertical Curve: It is a curve situated in the vertical plane; it joins the points of varying gradient along a road and railway (as well as duct and pipeline).
Important Definitions concerned with Curve Surveying:
Point of Intersection (PI): The Point of Intersection is the point where the back and forward tangents intersect each other. A survey station is setup at this point. Intersecting Angle
(I): The Intersecting Angle I is equal to Deflection Angle at PI. The surveyor either computes its value from the preliminary traverse station angles or measures it in the field
.Radius (R): The Radius is the radius of the circle of which that curve is an arc
.Point of Curvature (PC): The Point of Curvature is the point where the circular curve begins. The back tangent is tangent to the curve at this point.Point of Tangency
(PT): The Point of Tangency is the end of the curve where the path gets straight. The forward tangent is tangent to the curve at this point
.Length of Curve (L): The Length of Curve is the distance from the PC to the PT measured along the curve.Tangent Distance (T)
: The Tangent Distance is the distance along the tangents from PI to PC or from PI to PT. These distances are equal on a simple horizontal curve.
Central Angle (C): The Central Angle is the angle formed by the two radii drawn from the center of the circle (O) to the PC and PT. The Central Angle is usually equal (in value) to the angle.
Long Chord (LC): The Long Chord is the chord formed between PC and PT.
External Distance (E): The External Distance is the distance from PI to Midpoint Middle Ordinate (M): The Middle Ordinate is the distance from the midpoint of the curve to the midpoint of the long chord.
Degree of Curve
; also known as Curvature (D): The Degree of Curve defines the “sharpness” or “flatness” of the curve. There are two definitions commonly used for Degree Of Curve: “Arc Definition” and “Chord Definition”.
Chord Definition:
It is same as the Arc Definition except the formula for calculating the Radius (N. B: The term “ Chord Definition” is mostly used in Railway Curve Surveying). Radius is computed by this formula: …………. (i)
The Radius and Degree of Curve are not inversely proportional in Chord Definition (as they were in the Arc Definition). The shorter the radius, the sharper the curve and vice-versa. The Chord Definition is used primarily for railroads in Civilian Practice and for both roads and railroads in Military Practice. In metric system, using a chord of 30.48 meters long, surveyor computes radius by the formula of eq. R = 1746.40 mChords:
by locating the center of the circle, swinging the arc with a tape. The surveyor lays out these curves by staking the ends of a series of chords (Fig. 3-4). Since the ends of the chords lie on the circumference of the curve, surveyor defines the arc in the field. To reduce the discrepancy between the arc distance and chord distance, the surveyor uses the following chord lengths:
Types of Circular Curves
Reverse Curves
A tangent is also placed between the two curves in Reverse Curve
Spiral Curves
Compound Curves

Simple Curve
Spiral curves are typically placed between the tangents and circular curves to provide a transition from a normal crown section to a super-elevated oneSpiral curves are used at intersections to increase the room for long trucks to make easy turning movement, usually in the urban area. 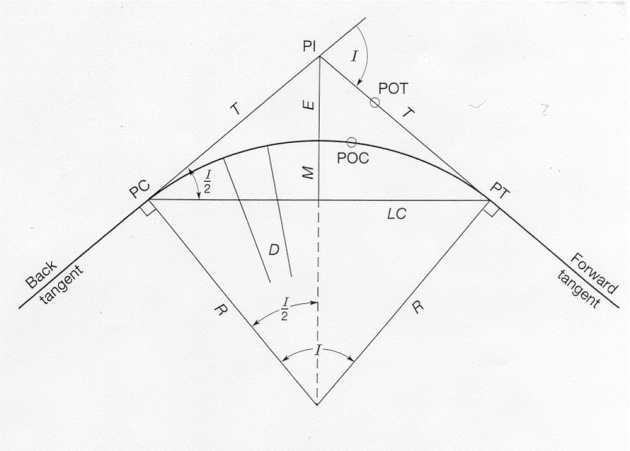
Consider the figure (Fig.1) given on the previous slide: The Def. Points PC, POC and PT are denoted as A, F’ and C representing a simple (horizontal) curve in Plan View; where R = Radius of the curveθ = Angle of intersection of the two tangents T and T i.e. ABCI = Angle of DeflectionGA = Line of Back TangentCH = Line of Forward Tangent LC = Chord of the curve = Straight Line ACPC = Starting Point of Curvature or Tangent Curve Point PT = End Point of Tangency or Tangent Curvature PointAB = BC = T = Tangent Distance or Tangent LengthBF = External DistanceEF = Mid-ordinate or VerSin (= versed sine of the curve which is equal to 1 – Cos of an angle)AFC = Rightward curve i.e. curve deflected rightwardFrom Fig.1: Angle of Intersection i.e. the angle formed at point PI ( ABC) + Angle of Deflection ( CBK) = θ/2 + θ/2 + I = θ + I = 180o CBK = 180o – θ = I = Angle of Deflection Central Angle ( O) = Angle of Deflection ( I) Tangent Length AB = BC = T = AE.SecI/2 and R = AE.CosecI/2 [AE = R.Sin(I/2)] Length of the chord = AC = AE + EC = 2AE = 2[R.Sin(I/2)] = 2R.Sin(I/2)Length of the arc AFC = R[/180o]I = RI/180o [OB = R.Sec(I/2)] Apex of the curve BF = External Distance = OB – OF = R.Sec(I/2) – R= R[Sec(I/2) – 1] [Considering OAB = 90o SecI/2 = OB/OA = OB/R]Mid-ordinate = EF = OF – OE = R – R.Cos(I/2) = R[1 – Cos(I/2)] = R.Ver.Sin(I/2)[Length of arc = 2Rθ/360o = Rθ/180o where R is radius and θ is subtended angle]Radius and Degree of Curve: From Figure 1: A curve is specified either by Radius R or Degree of Curve D (also known as Curvature) subtended at the centre of chord of a particular length. In Pakistan, the average length of the said chord is usually kept 30 m (100 ft). Relationship between R and D is given by: Let chord AC = 30 m E is the mid-point of the chordIn OAE: OA = R; and AE = EC = 15 m AOE = I/2SinI/2 = AE/OA = 15/R R = 15/(SinI/2)When SinI/2 is small, SinI/2 will be equal to I/2 in radians. So: 15 15 x 360o 1718.87 [R = AE / (θ/180o) = AE.360o/ θ] R = ---------------------- =----------- = ---------- (I/2) x (/180o) I IThis is a general formula showing the relation between R and I of a Simple Curve.



