Super-elevation: Although the transition curves can reduce the effect of radial force on a vehicle; this can also be further reduced or even eliminated by raising one side of the road relative between the two sides of the road is known as the Super-elevation (SE).

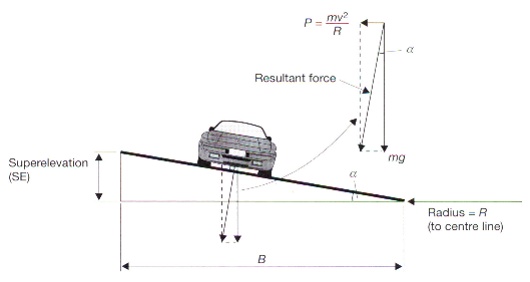
In theory, by applying enough super-elevation the resultant force is made to
act perpendicular to the surface of the road pushing the vehicle down rather than throwing it off.  SE = B tan

Therefore; maximum theoretical super-elevation SEMax = Bv2/gR where v is the velocity of vehicle in m/s and B is the horizontal length of super-elevation.
The maximum SE (i.e. SEMax) occurs when & where the radius r = R, along the central arc of a composite curve or at Tc on a wholly transitional curve.
In practice for the roadways with fast design speeds, wide carriageways or small radii, SEMax could be very large and would be alarming to drivers approaching it and dangerous with reduced speeds.
Therefore the following best practice rules are generally applied:
(i) Super-elevation shall normally balance out only 45% of the radial force P (i.e. SE = 0.45(Bv2/gR)).
(ii) In rural areas super-elevation shall not exceed 7% (1 in 14.5 and wherever possible, radii should be chosen such that super-elevation is kept within the desired value of 5% (1 in 20).
(iii) In urban areas, super-elevation shall not exceed 5%
The minimum allowable SE is 2.5% (1 in 40) to allow for drainage.
Expressing v in kph and R in metres and substituting gravity for 9.81m/s2 gives: Maximum allowable SE = Bv2 / 282.5R
Types of Transition Curve: There are two types of curves used to form the transitional section of a Composite Curve or Wholly Transitional Curve. These are: (i) The Clothoid (ii) The Cubic Parabola
For a transition curve the equation r.l = K applies here i.e. the radius r must be reduced in proportion to the length l. This is the property of a spiral and one curve, which has this property is the Clothoid.
Another common curve derived from the Clothoid is the Cubic Parabola which is not a spiral i.e. r.l is not always constant. However it can be used over a certain range and is less complex than the Clothoid
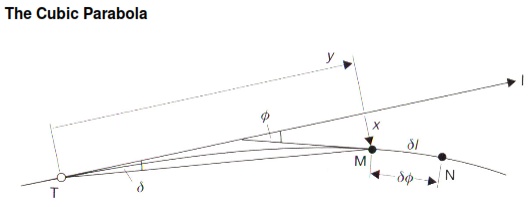
The Clothoid: The equation of the clothoid can be derived from the above diagram, which shows the two points close together (M and N) on a transition curve of length LT.
F is the deviation angle between the tangent at M and the straight TI
δ is the tangential angle to M from T with reference to TI
l is the length from point T to any point M on the curve (not shown)

The Clothoid: This is the basic equation of the
The Cubic Parabola is not a true spiral curve and cannot always be used. It approximates very close to a spiral curve, however, and can be used within a certain range of deviations angle. Practically, it can be set-out easier than a Clothoid and hence it is more commonly used.

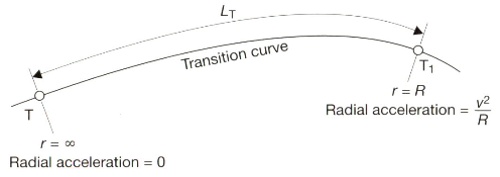
The length of a Transition Curve Required to Minimise the Passengers and Vehicles Discomfort: Transition curve lengths must be designed so that they should minimise the passengers and vehicles discomfort At any point the radial force P = mv2/r but since force = mass x : c = v2/r i.e. the faster the change in radius the faster the change in c and therefore the faster radial force is exerted resulting in passenger discomfort and safety risks.
and maximise the comfort and safety. Consider the curve below:

Tangent Lengths and Total Curve Lengths: In order for a composite cure to move vehicles through the deflection angle θ, each transition curve must move them through a further deflection Φmax.
Setting out Composite and Wholly Transitional Curves:
The centre line provides an important reference on site from which other features can be established and it can be set out either by traditional or coordinate methods.
Setting out using the Tangential Angles Method: Setting out for tangential curves is similar to the method used for circular curves.
This is the most accurate of the traditional methods and it can be used for any transition curve. It is undertaken using a theodolite and a tape and, as with the circular curves method it is necessary to first set out the intersection point I. The method by which this is done is identical to that used for circular curves. Once the intersection point has been fixed, tangent points T and U can be obtained by