The flux is a property of a vector field. The word flux comes from a Latin word meaning to flow and it is appropriate to think of flux of particular vector as being a measure of the flow or penetration of the field vectors through an imaginary fixed surface in the field. The velocity field represents the fluid flow, the field itself does not flow but is a fixed representation of the flow.

Imagine we place into the stream a wire bent into the shape of a square loop of area A. The square is placed so that its plane is perpendicular to the direction of the flow. In our analysis of fluid flow we replace the actual motion of fluid particles by the velocity field associated with the flow. Therefore we can consider either the actual flow of material particles through the loop or the flux of the velocity field through the loop.

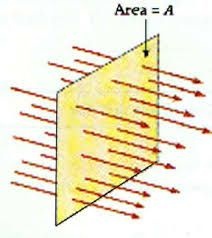
The magnitude (f) of the flux of velocity field through the loop of area A is written in the form of volume rate of fluid flow as:
                               |f| = vA
in which v is the magnitude of the velocity at the location of the loop. The flux on the one hand be considered as the measure of the rate at which the fluid passes through the loop. However in terms of field concept flux can be considered as a number of field lines passing through the loop.

Now if the loop is rotated so that it is no longer perpendicular to the direction of the velocity. Note that the field lines now passing through the loop are less and the area of the square is AcosQ (Q is the orientation).

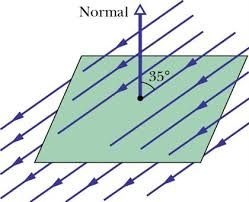
Thus the magnitude of the flux is:
                               |f| = vAcosQ
If the loop were rotated so that the fluid velocity were parallel to its surface then Q = 90 and thus:
                               |f| = 0
Note that in this case no field lines pass through the loop.